Reconstitution de figures, manipulations des puzzles
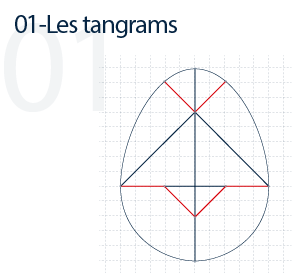
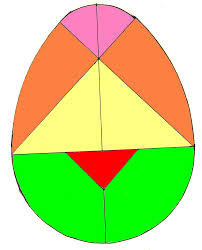
► le tangram « classique » et ceux de la même famille : paratonnerre, brise-croix, cœur brisé, œuf magique…
► le Sam Loyd
► le loculus d’Archimède
►Tangrams classiques et autres de la même famille
Quelques exemples :
►Le Sam Loyd
Sam Loyd (1841- 1911) a produit de nombreux casse-tête.
Les 5 pièces de ce puzzle permettent de reconstituer d’autres figures géométriques simples notamment :
- un carré
- un rectangle
- un parallélogramme
- un triangle rectangle
►Le loculus d’Archimède
Ce puzzle, découvert en 1906 sur un palimpseste (parchemin réutilisé) est constitué de 14 pièces. On peut reconstituer ce carré de 17152 façons différentes (résultat trouvé très récemment : 2003). Archimède avait-il dénombré toutes ces solutions ?
Autre particularité : Si l’aire du petit triangle vert marqué d’une étoile est 1, les autres pièces ont des aires entières de 1 à 8.
Activités proposées lors de l’atelier de l’exposition
Construction de puzzles ( sur feuilles blanches ou à partir d’un réseau ), agrandissement des pièces.
Une série d’activités ou d’exercices extraites du document 2 :
- travail sur les formes géométriques
- travail sur aires et périmètres
- travail sur agrandissement / réduction
- travail sur les fractions
- travail sur le dénombrement …
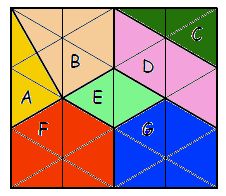
Exemple :
Ce puzzle est formé de 7 pièces de 5 formes différentes. Quel est le nom de chacune de ces 5 formes ?
Si l’aire d’un triangle équilatéral du réseau est 1, quelle est l’aire de chacune des pièces ?
Mobilier pour la salle d’exposition