Peut-on démontrer avec des puzzles ?
TRAME DES 3 PANNEAUX
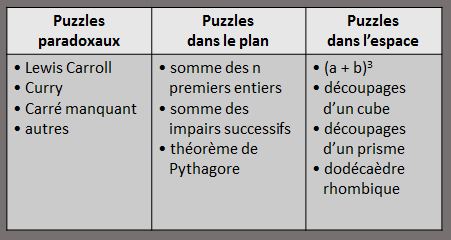
► Puzzles paradoxaux
-
Lewis Carroll : 441 = 442 ?
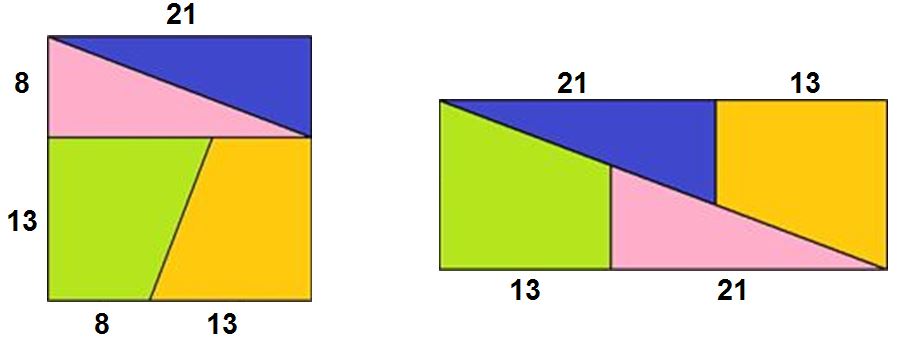
21 x 21 = 441 13 x 34 = 442
Cherchez l’erreur !
-
Triangle de Curry
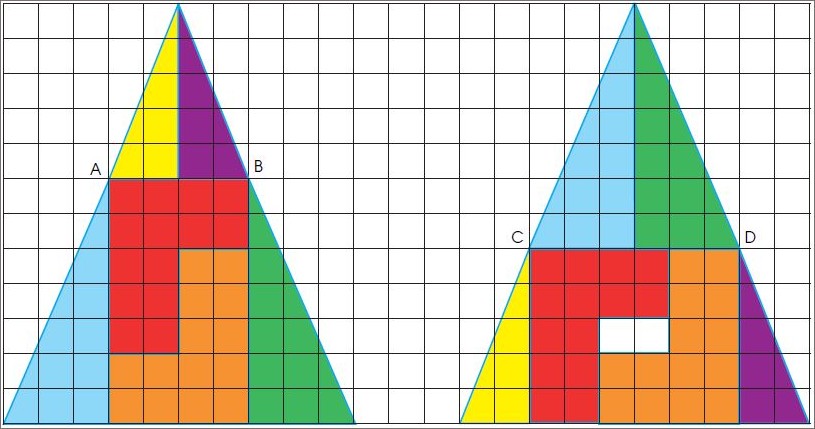
Pourquoi ce trou dans le triangle de droite ?
-
Le carré manquant
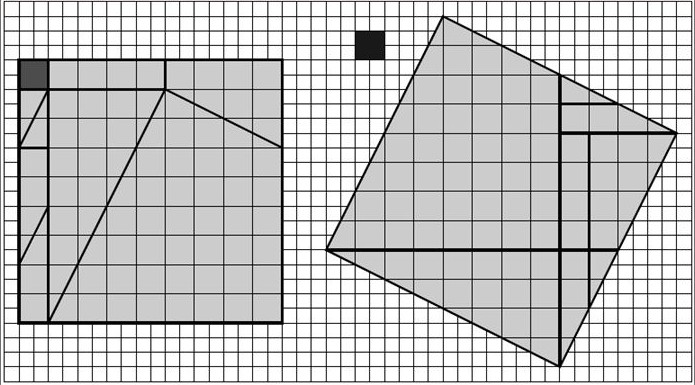
Avec les pièces grises du carré de gauche, on construit un carré de même taille à droite, mais sans utiliser le carré noir.
Bizarre !
► Puzzles dans le plan
Les puzzles qui suivent constituent de véritables démonstrations ou seulement des illustrations d’un théorème.
-
Somme des n premiers entiers
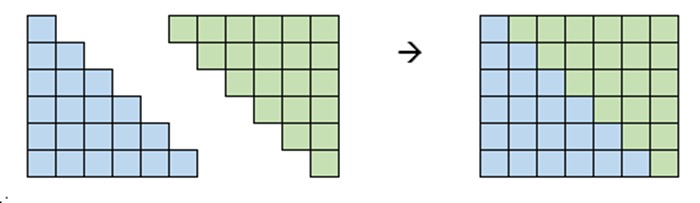
2 × (1 + 2 + 3 + 4 + 5 + 6) = 6 × 7
1 + 2 + 3 + 4 + 5+ 6 = (6 × 7)/2
Se généralise sans difficulté
-
Somme des impairs successifs
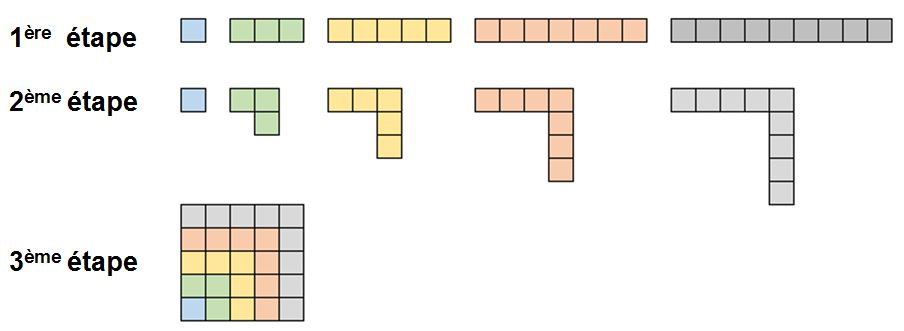
1 + 3 + 5 + 7 + 9 = 5²
Se généralise sans difficulté
-
Autre présentation (1)
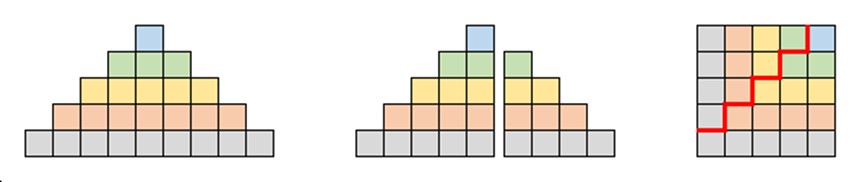
-
Autre présentation (2)
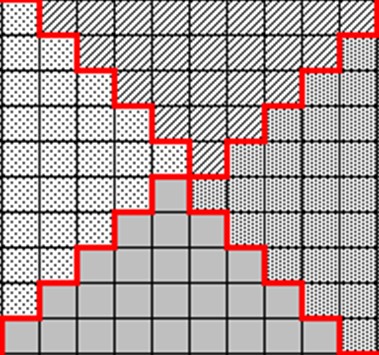
4 × (1 + 3 + 5 + 7 + 9) = 4 × 5²
-
Théorème de Pythagore
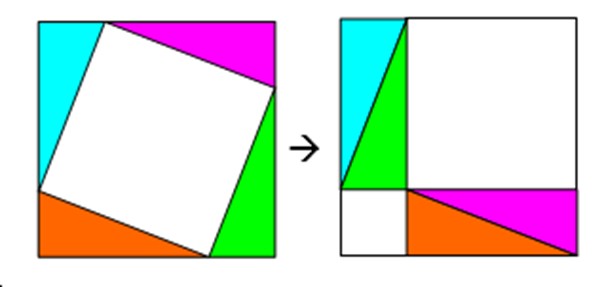
► Puzzles dans l’espace
-
(a + b)³ = a³ + 3a²b + 3 ab² + b³
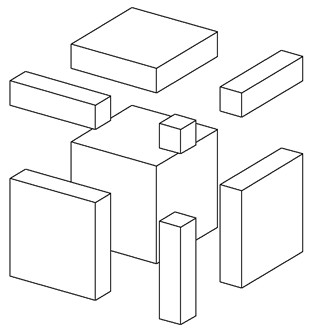
découpage du cube en 8 pièces :
– un cube de côté a
– un cube de côté b
– 3 parallélépipèdes de côtés a, a et b
– 3 parallélépipèdes de côtés a, b et b
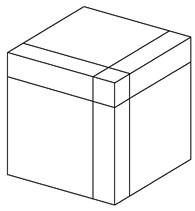 →
→ 
-
Découpages d’un cube (illustrant le volume d’une pyramide)
 →
→ 
-
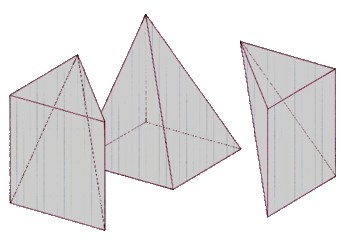
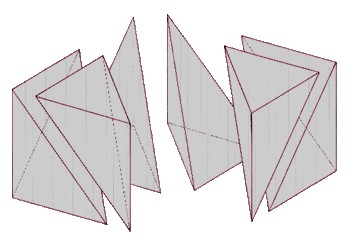
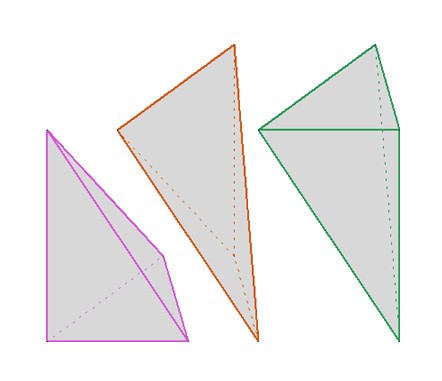
Découpage d’un prisme droit en 3 pyramides, dont 2 sont identiques
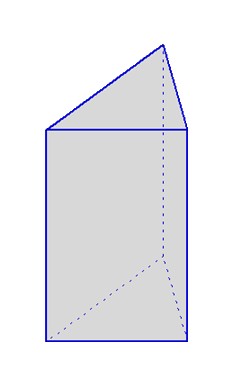 →
→ 
-
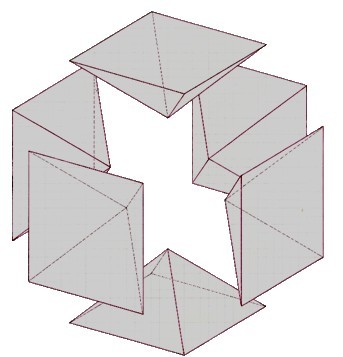
Découpage d’un cube en 6 pyramides à base carrée
-
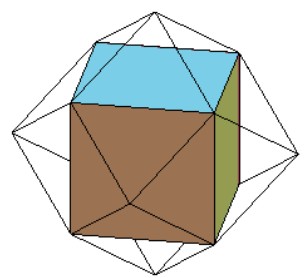
Dodécaèdre rhombique
En collant les faces carrées de ces pyramides sur les faces du cube, on obtient le dodécaèdre rhombique (que l’on retrouve dans les alvéoles des ruches d’abeilles, les baies de grenade et dans beaucoup de situations intéressantes étudiées par Kepler)