Une illustration : design et ameublement

► Panneau 1 : Reconstituer un carré ou un rectangle avec des carrés insécables de dimensions différentes entières

Panneau :
Historique du problème
Quelques réponses
Manipulations : carrés et rectangles
Cas des cubes (espace)

• Faire un carré avec des carrés

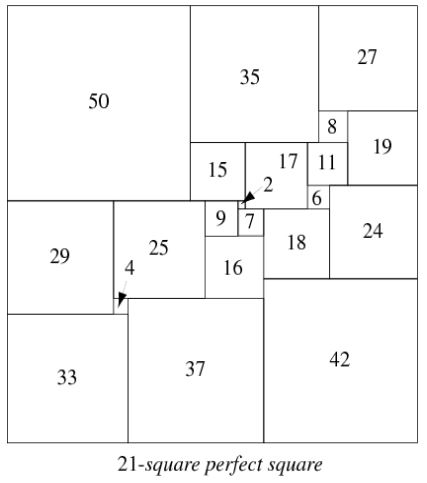
• Faire des rectangles avec des carrés

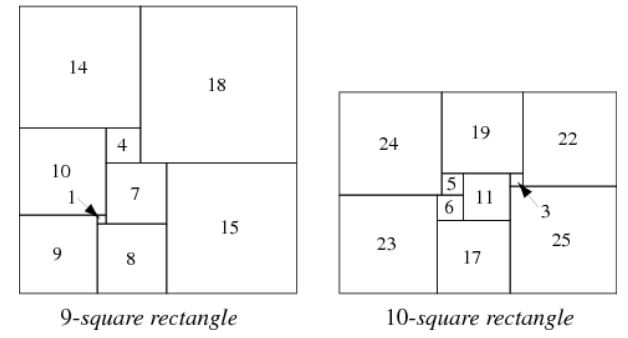
Différents niveaux :
– Manipulations, les petits carrés étant donnés
– Raisonnement + manipulations, les petits carrés étant donnés
– Quelles sont les dimensions des côtés des rectangles pouvant être reconstitués avec des carrés de différentes dimensions
– Dans l’espace, est-ce possible avec des cubes ?

►Panneau 2 : Faire un carré avec des carrés sécables de même taille

Panneau :
Quelques exemples historiques
Quelques réponses
Manipulations

• Avec 2 (Ménon, …), avec 3 (Abul Wafa, …)

       

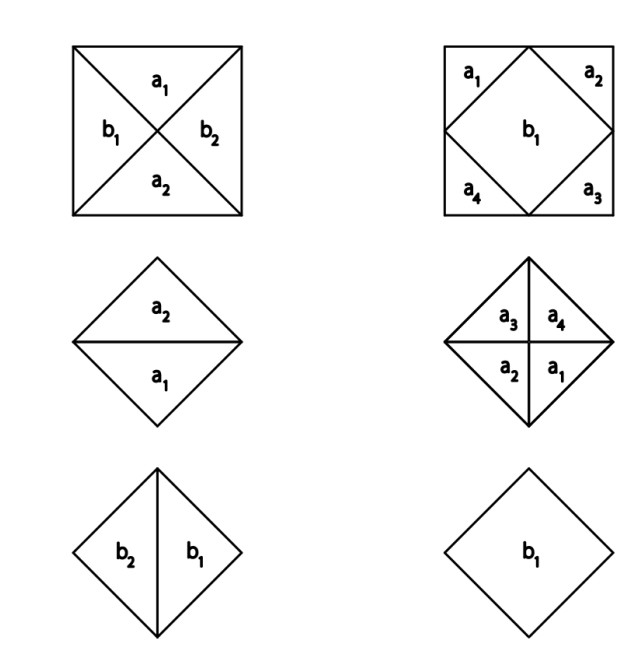
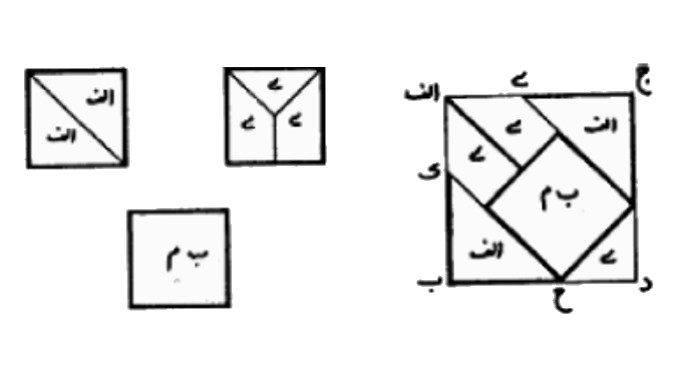
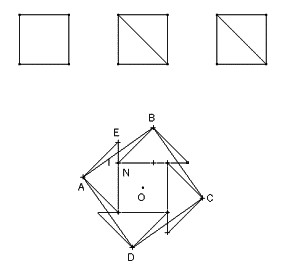
Différents niveaux :
– Constructions
– Manipulations
– Démonstrations
– Généralisation avec n carrés
– Recherche du plus petit nombre de morceaux

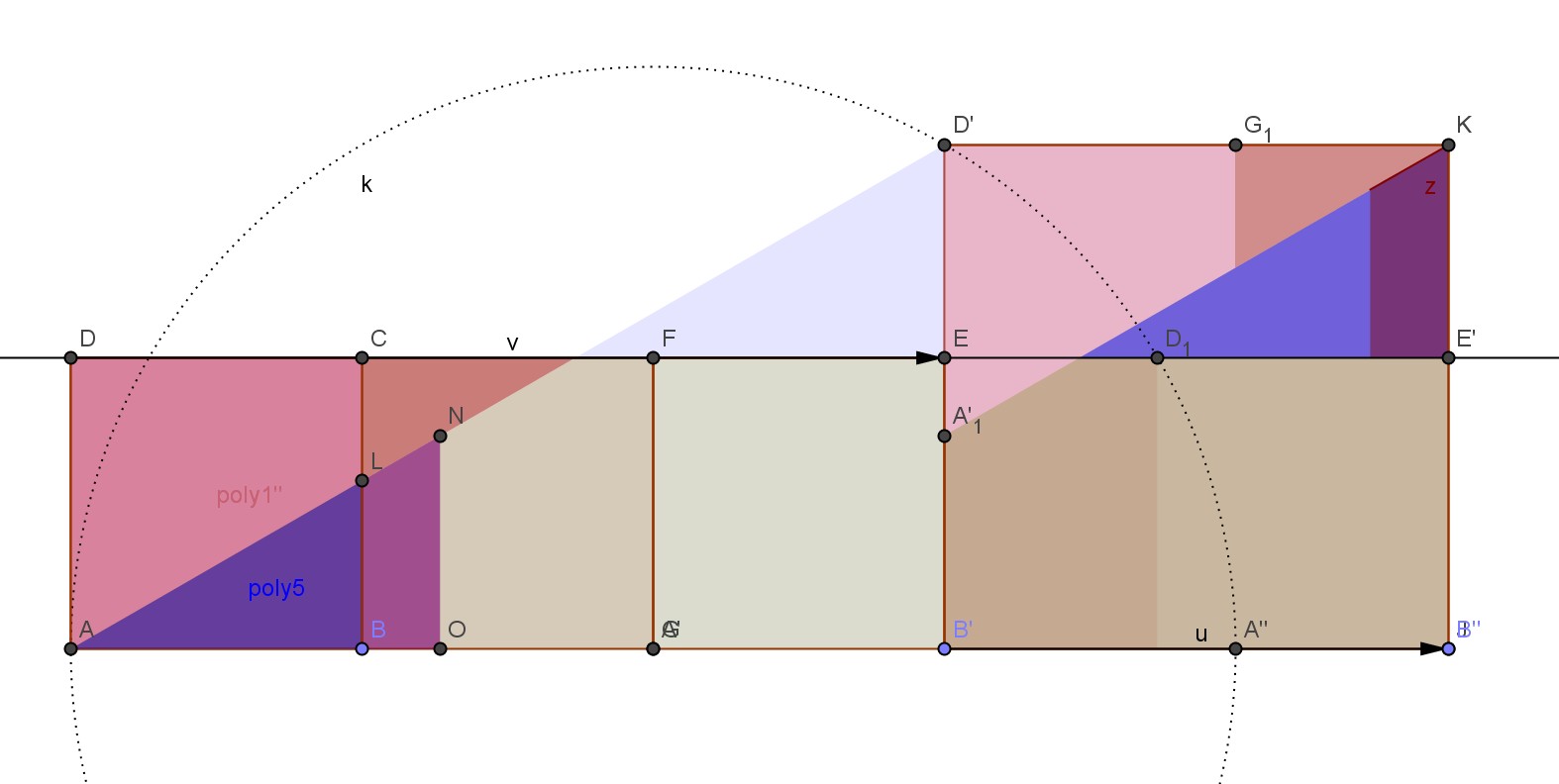
• Avec 5 carrés

    

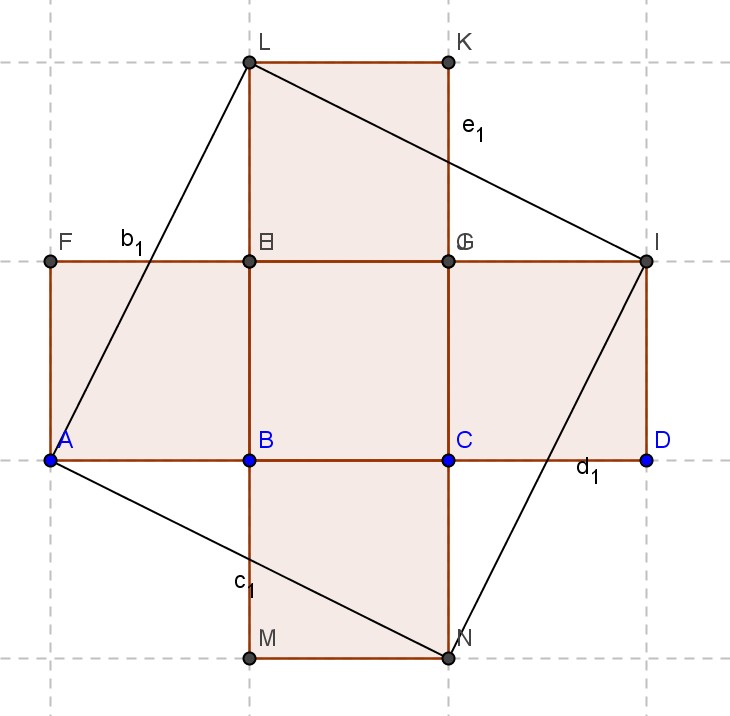
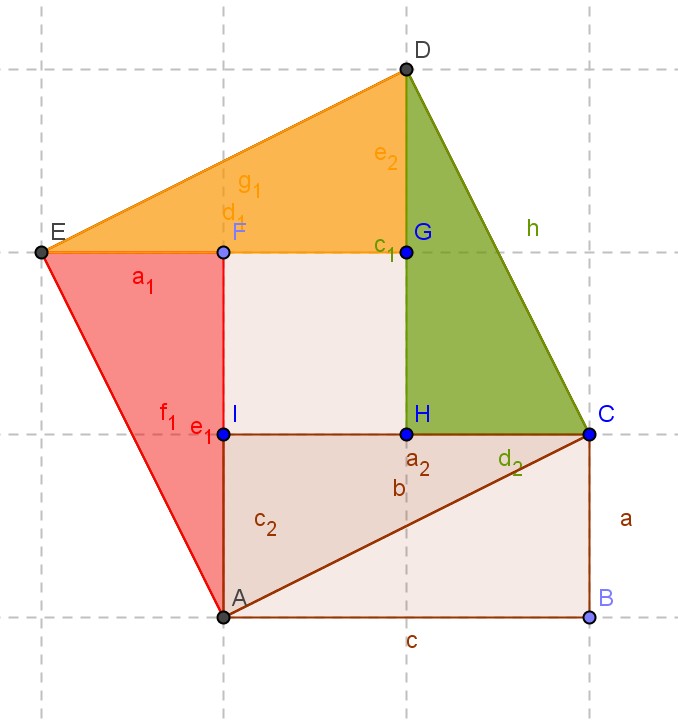
►Panneau 3 : faire un carré avec  des carrés de tailles différentes, théorème de Pythagore

Panneau :
Pythagore et son histoire
Découpages chinois
La recherche du nombre minimal de pièces

     

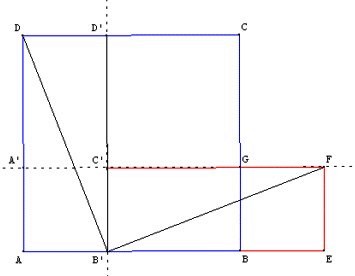
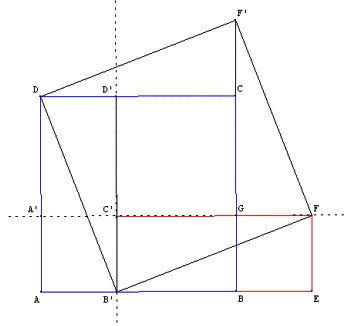
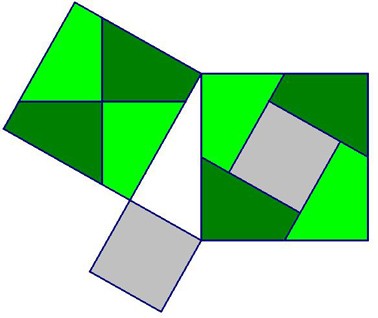
– Manipulations
– Constructions
– Démonstrations
– Recherche du nombre minimal de pièces,
– Avec trois carrés de tailles différentes, etc.

►Bar à casse tête

Faire un carré avec  des carrés insécables pouvant avoir la même dimension  (à partir de carrés donnés)

   

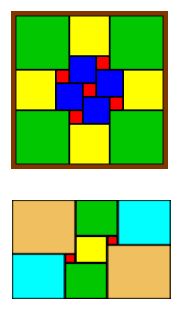
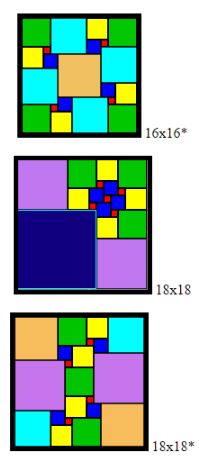
►Atelier  découpage

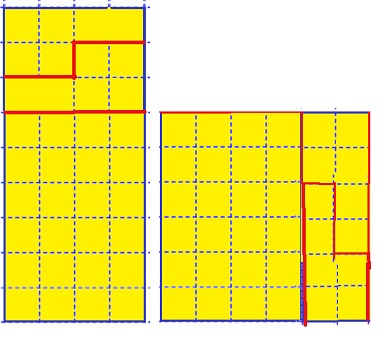
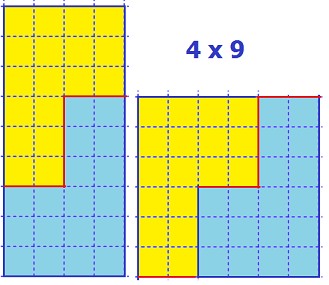
1- Découper un rectangle  sur quadrillage pour faire un carré

• Activité en ligne sur le site « Les Mathématiques.net »

    

2- Le côté n du carré étant donné, trouver le nombre minimal de carrés pour le reconstituer.

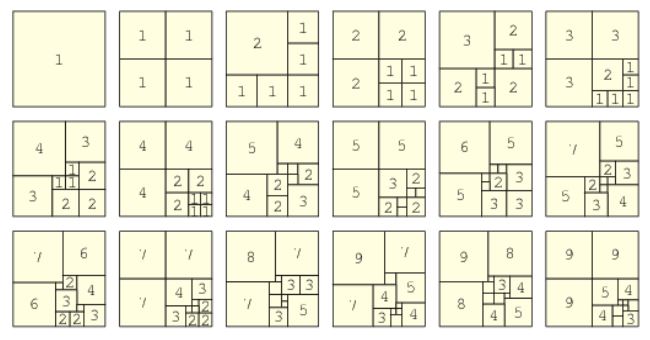
Manipulations avec des petits carrés de différentes dimensions et des gabarits.

• Activités en classe

3- Retrouver les pièces du puzzle

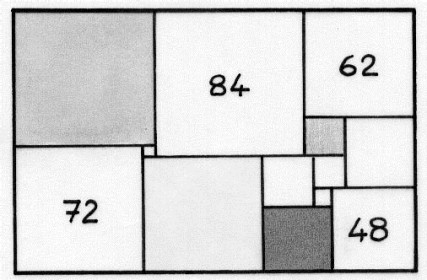
La figure ci-dessous est un rectangle constitué de 13 carrés. Les longueurs des côtés des carrés sont des nombres entiers de millimètres tous différents. Chacun des quatre nombres donnés indique la longueur du côté du carré dans lequel il est inscrit.

Retrouver la longueur des côtés des autres carrés.
Reproduire la figure en grandeur réelle et indiquer pour chaque carré la longueur de son côté.

—

Thèse de Ian Gambini « Quant aux carrés carrelés »

Retour accueil